เมื่อกล่าวถึงทฤษฎีเกม (Game Theory) ซึ่งเป็นเครื่องมือทางคณิตศาสตร์ในการวิเคราะห์การมีปฏิสัมพันธ์ในสังคม ผู้คนมักนึกถึงเกมแบบคลาสสิก อย่างเช่น เกมทางแพร่งของนักโทษ (Prisoner’s Dilemma) หรือการมีปฏิสัมพันธ์กันของหน่วยผลิตในตลาดผู้เล่นสองราย (Duopoly Market) เอาเข้าจริงแล้ว ยังมีรูปแบบเกมอีกหลายอย่างที่ใช้เพื่ออธิบายปรากฏการณ์ต่าง ๆ ในชีวิต เช่น เกมล่ากวาง (Stag Hunt) เกมไก่อ่อน (Chicken Game) เกมหนุ่มสาว (Battle of Sexes) ไปจนถึงเกมที่ใช้อธิบายความสัมพันธ์ระดับประเทศอย่างเกมสะสมหัวรบนิวเคลียร์ที่ผู้คนคุ้นเคย อย่างไรก็ตาม ถ้าหากเราพยายามมองไกลตัวออกไปจากสังคมของ Homo Economicus และ Homo Sapian เช่น ลองมองไปบนสนามหญ้า หรือในสระน้ำ เครื่องมือทฤษฎีเกมก็ยังคงสามารถนำเราไปศึกษาปรากฎการณ์ที่ไม่ได้มีแค่การตัดสินใจของมนุษย์

ตัวอย่างที่จะเล่าต่อไปซึ่งเป็นเรื่องราวของการขยายเผ่าพันธุ์ของกิ้งก่าสายพันธุ์ Side-blotched lizards (หรือชื่อตามอนุกรมวิธาน Uta stansburiana) จากงานศึกษาของ Sinervo และ Lively ในปี 1996 ซึ่งเป็นตัวอย่างที่น่าสนใจในทฤษฎีเกมเชิงวิวัฒนาการ กิ้งก่าสายพันธุ์นี้มีการจับคู่และทำรัง โดยมีเพศเมียที่มีลายสีเหลืองที่คอ และมีเพศผู้ที่มี 3 ประเภท ได้แก่ ประเภทแรกคือมีลายสีส้มที่คอ มีพฤติกรรมก้าวร้าว และสามารถครอบครองพื้นที่อยู่อาศัยได้มากที่สุด ประเภทที่สองคือมีลายสีน้ำเงินที่คอ ซึ่งมีพฤติกรรมก้าวร้าวที่น้อยกว่าสีส้ม ครอบครองพื้นที่อยู่อาศัยน้อยกว่าประเภทแรก และมีพฤติกรรมเฝ้ารังซึ่งมีเพศเมียที่เป็นคู่อาศัยอยู่ ส่วนประเภทที่สุดท้ายคือมีลายสีเหลืองที่คอ (ซึ่งมีลักษณะคล้ายกับเพศเมีย) ประเภทที่สามไม่ได้ใส่ใจกับการครอบครองอาณาเขตมากนัก แต่ด้วยลักษณะของมันนี่เองทำให้มันใช้การปลอมตัวและเนียนแอบเข้าไปผสมพันธุ์ตามรังของชาวบ้าน

หากเราทำการเปรียบเทียบกิ้งก่าทั้ง 3 ประเภทในสายพันธุ์ จะพบว่าเพศผู้ที่มีลายสีส้มที่คอจะครอบครองพื้นที่ และได้คู่เพศเมียมากกว่า หรือชนะกิ้งก่าลายสีน้ำเงิน แต่กลับแพ้กิ้งก่าที่มีลายสีเหลืองที่แอบย่องไปหาคู่รักของมันเนื่องจากไม่มีพฤติกรรมเฝ้ารัง กิ้งก่าลายสีน้ำเงินจะแพ้กิ้งก่าสีส้มในด้านพื้นที่อยู่อาศัยและคู่ครอง แต่ชนะกิ้งก่าสีเหลืองจากพฤติกรรมหวงรังของมัน ส่วนกิ้งก่าสีเหลืองจะแพ้กิ้งก่าสีน้ำเงินจากการที่มันไม่สามารถย่องเงียบเข้าหาคู่รักชาวบ้านได้ แต่ชนะกิ้งก่าสีส้มในการแอบย่องเข้ารัง

นอกจากนี้ การแข่งขันนี้ยังก่อให้เกิดวัฏจักรของกิ้งก่าเพศผู้แต่ละประเภทที่จะผลัดเปลี่ยนสัดส่วนประชากรในพื้นที่ เช่น หากในปีที่ 0 มีกิ้งก่าสีส้มเยอะ ปีที่ 1 กิ้งก่าสีเหลืองจะเพิ่มจำนวน ในขณะที่กิ้งก่าสีส้มลดลง ปีที่ 2 กิ้งก่าสีน้ำเงินจะเพิ่มจำนวน ในขณะที่กิ้งก่าสีเหลืองลดลง ปีที่ 3 กิ้งก่าสีส้มจะเพิ่มจำนวน ในขณะที่กิ้งก่าสีน้ำเงินจะลดลง แล้วเกิดเหตุการณ์วนกลับมาเริ่มต้นเหมือนปีที่ 0 อีก แม้ว่าการศึกษาจะแสดงให้เห็นว่าสัดส่วนกิ้งก่าเพศผู้บางประเภทลดลงน้อยจนแทบจะสูญพันธุ์ในช่วงที่ประชากรลดลง แต่มันก็ยังสามารถเพิ่มประชากรกลับมาและดำรงวัฏจักรเดิมต่อไปได้ หากลองวิเคราะห์ดูสักพัก แล้วลองนึกถึงชีวิตในวัยเด็กจะพบว่า สิ่งนี้มีความคล้ายคลึงกับการเล่นเป่ายิงฉุบ หรือ Rock-Paper-Scissors ค้อนชนะกรรไกร แต่แพ้กระดาษ กระดาษชนะค้อน แต่แพ้กรรไกร ส่วนกรรไกรชนะกระดาษ แต่แพ้ก้อนค้อน วนกันไปมาเหมือนกับกิ้งก่าเพศผู้ทั้ง 3 ประเภท และสามารถเขียน Matrix ผลลัพธ์ได้ดังรูป โดยกำหนดให้ 0 คือเสมอ 1 คือชนะ และ -1 คือแพ้

เกมนี้แม้จะเป็นเกมที่เด็กเล่นได้โดยเข้าใจกฎของเกมและเลือกกลยุทธ์ได้ แต่กิ้งก่าไม่สามารถเข้าใจและเลือกกลยุทธ์ได้ก็ตาม แต่จากรูปข้างต้น ทั้งเด็กและกิ้งก่าก็มีความเหมือนกันในเชิงกลยุทธ์ดังที่ J. McKenzie Alexander ได้กล่าวในหนังสือ Evolutionary game theory สิ่งเหล่านี้ล้วนชี้ให้เกิดคำถามที่สำคัญต่อไปคืออะไรกันเป็นกลไกที่ทำให้กิ้งก่ามีการตอบสนองต่อกันที่เหมือนกับการเป่ายิงฉุบในเชิงกลยุทธ์ คำตอบคงต้องเป็นสิ่งที่มีส่วนเกี่ยวของในการกำหนดพฤติกรรม สัญชาตญาณ และร่างกายของสิ่งมีชีวิตในขั้นพื้นฐาน ดังที่ Richard Dawkins ได้นำเสนอในผลงาน The Selfish Gene และสิ่งนั้นก็คือยีน (Gene) หรือกลุ่มสารพันธุกรรมซึ่งเป็นลำดับของเบสที่เรียงกันเป็นเกลียวคู่ และถูกถอดรหัสออกมาเพื่อออกคำสั่งต่าง ๆ ในระดับเซลล์ไปจนถึงการดำรงชีวิตของสิ่งมีชีวิต และมีปฏิสัมพันธ์กับสิ่งแวดล้อม แน่นอนว่าสิ่งเหล่านี้เกิดการแข่งขันอย่างเห็นได้ชัดผ่านการส่งต่อยีน ดังเช่นทฤษฎีวิวัฒนาการ ยีนที่สามารถส่งต่อตัวเองไปสู่รุ่นอนาคตจะถือว่ามีศักยภาพและถูกเก็บไว้ หากมองผ่านมุมของทฤษฎีเกม การคัดเลือก และส่งต่อยีน ก็สามารถนำทฤษฎีเกมเข้าไปเป็นเครื่องมือวิเคราะห์ได้เช่นกัน

ในที่นี้ลองสมมติตัวอย่างเกม Hawk-Dove ที่คิดโดย John Maynard Smith จากหนังสือ Evolutionary game theory ของ J. McKenzie Alexander โดยให้มียีน 2 แบบในการแสดงพฤติกรรม แบบแรกคือยีนกลัว โดยจะแสร้งทำเป็นสู้แต่จะหนี (Dove) แบบที่สองคือยีนสู้โดยสู้จริง (Hawk) ทั้งสองกำลังแย่งชิงทรัพยากรกัน กำหนดให้ต้นทุนการสู้คือ C และทรัพยากรที่จะได้คือ V หากทั้งสองสู้กันเอง (Hawk, Hawk) ต่างฝ่ายจะเกิดการสูญเสีย และได้ผลตอบแทน (Payoff) เท่ากับ ((V-C)/2,(V-C)/2) ซึ่งหมายถึงการแบ่งทรัพยากรที่หักต้นทุนการสูญเสีย ถ้าหากฝ่ายใดฝ่ายหนึ่งสู้ แต่อีกฝ่ายหนี จะได้ผลตอบแทน (Payoff) คือ ถ้าหากสู้จะได้ V แต่ถ้าหากหนีจะไม่ได้อะไรเลยหรือมีค่าเป็น 0 หรือกล่าวได้ว่าจะมีฝ่ายที่ได้รับทรัพยากรเต็มกับฝ่ายที่ไม่ได้เลย และถ้าหากทั้งสองฝ่ายหนี (Dove, Dove) ต่างได้รับผลตอบแทน (Payoff) เป็น (V/2,V/2) ซึ่งเป็นการแบ่งทรัพยากรกันเองโดยตรง ผลตอบแทนของแต่ละทางเลือกสามารถเขียนในรูปของเมทริกซ์ได้ดังนี้

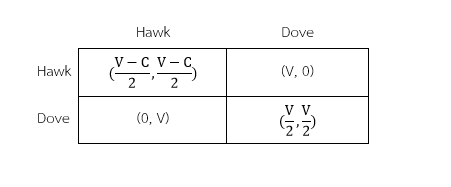
หากมองว่ากำไรมากกว่าต้นทุน (V>C) โดยสมมติให้ V=4, C=2 จะพบว่ายีน Hawk จะเด่นขึ้นคล้ายกรณีเกม Prisoner’s Dilemma และข่มยีน Dove อย่างสมบูรณ์ (1>0 และ 4>2) ซึ่งทำให้ยีน Hawk จะเป็นยีนที่มีในประชากรทั้งหมด และมีกลยุทธ์ดุลยภาพแนชโดยแท้ (Strict Nash Equilibrium Strategy) ซึ่งควรจะเพียงพอต่อการเกิดเสถียรภาพในวิวัฒนาการแล้ว อย่างไรก็ตาม ไม่จำที่จะต้องเกิดกรณีเช่นนี้เสมอไป

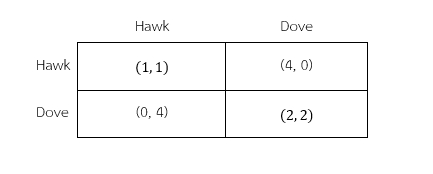
แต่ถ้าหากมองในกรณีต้นทุนมากกว่ากำไร (V<C) โดยให้ V=2, C=4 ซึ่งมีโอกาสเกิดในธรรมชาติได้มากกว่าแล้ว การต่อสู้กันมักลงเอยด้วยชัยชนะพร้อมการบาดเจ็บหรือการแพ้พร้อมความตาย  ในสถานการณ์นี้จะพบว่าเกิดกลยุทธ์ผสม (Mixed Strategy) ซึ่งมีการใช้ความน่าจะเป็นมาคิดร่วมด้วยเพื่อหาผลตอบแทนที่คาดหมายในการใช้แต่ละกลยุทธ์  เมื่อทำการคำนวณตามแบบกลยุทธ์ผสมจะพบว่า ทั้งยีน Hawk และยีน Dove จะมีความน่าจะเป็นในการแสดงอยู่ที่ 0.5 และหากความน่าจะเป็นที่จะเล่น Hawk เพิ่ม (มากกว่า 0.5) จะส่งผลให้ยีน Dove เป็นตัวเลือกที่เหมาะสมกว่า เด่นขึ้น และส่งต่อได้ดีกว่า  แต่หากความน่าจะเป็นที่จะเล่น Hawk ลดลง (น้อยกว่า 0.5) จะส่งผลให้ยีน Hawk เป็นตัวเลือกที่เหมาะสมกว่า เด่นขึ้น และส่งต่อได้ดีกว่าเช่นกัน  ความน่าจะเป็นที่ 0.5 จะเป็นความน่าจะเป็นที่เป็นดุลยภาพสัดส่วนประชากรในเกมนี้ซึ่งเป็นกลยุทธ์เสถียรภาพเชิงวัฒนาการ (Evolutionary Stable Strategy: ESS) กล่าวคือสัดส่วนประชากรที่มียีนทั้งสองจะแบ่งกันครึ่งต่อครึ่ง  และหากสัดส่วนเปลี่ยน การเปลี่ยนแปลงในผลตอบแทนที่คาดหมายจะเปลี่ยนแปลงไป ซึ่งส่งผลให้สัดส่วนกลับมาที่ 0.5 เช่นเดิมตามในตัวอย่างนี้

ตัวอย่างล่าสุดนี้แสดงให้เห็นว่า ยีนที่กำหนดพฤติกรรม ซึ่งต่างจากตัวอย่างของกิ้งก่าเล็กน้อย ในแง่ที่เกม Hawk-Dove ทำให้เราเห็น Evolutionary Stable Strategy อย่างชัดเจนว่า ในกลุ่มประชากรนี้จะมีดุลยภาพสัดส่วนของประชากร และหากเกิดการเปลี่ยนแปลงสัดส่วนประชากร Payoff ใหม่จะแย่กว่า Payoff ที่ดุลยภาพเดิมเสมอ จึงทำให้เกิดการเปลี่ยนแปลงสัดส่วนประชากรจนกลับสู่ดุลยภาพเดิม ขณะที่ตัวอย่างของกิ้งก่านั้น ทำให้เราเห็นถึงการการผลัดกันแพ้ผลัดกันชนะของกิ้งก่าแต่ละประเภทที่เปลี่ยนแปลงแบบ Cyclic Dynamic หรือพลวัตของวัฎจักรที่สลับกันไปโดยไม่มีกลยุทธ์เด่น มีเพียงแต่กลยุทธ์ที่ชนะได้ ก่อนที่จะโดนแทนที่ต่อไปในอนาคต

References

Alexander, J. M. (2023). Evolutionary game theory. Cambridge University Press.

Binmoore, Ken. (2019). ทฤษฎีเกม: ความรู้ฉบับพกพา (พรเทพ เบญญาอภิกุล, ผู้แปล). พิมพ์ครั้งที่ 3. กรุงเทพฯ: Bookscape.

Dawkins, Richard. (2017). ยีนเห็นแก่ตัว (เจษฏา เด่นดวงบริพันธ์, ผู้แปล). พิมพ์ครั้งที่ 4. กรุงเทพฯ: มติชน.

Sinervo, B., Lively, C. The rock–paper–scissors game and the evolution of alternative male strategies. Nature 380, 240–243 (1996). https://doi.org/10.1038/380240a0