ความก้าวหน้าทางเทคโนโลยีที่ขับเคลื่อนโดยข้อมูลกลายเป็นเมกะเทรนด์ (MegaTrend) หรือเปรียบเสมือนการค้นพบแหล่งน้ำมันใหม่ (สำนักงานพัฒนาวิทยาศาสตร์และเทคโนโลยีแห่งชาติ, 2020) ธุรกิจที่สามารถเติบโตได้อย่างยั่งยืนจำเป็นต้องเข้าใจลูกค้าอย่างถ่องแท้ ข้อมูลจึงเป็นสิ่งที่สำคัญอย่างยิ่ง (Kihn, 2025) การตัดสินใจด้วยข้อมูล (Data-Driven Decision Making) ย่อมดีกว่าการตัดสินใจโดยใช้สัญชาตญาณเพียงอย่างเดียว

การตัดสินใจบนพื้นฐานข้อมูลประกอบด้วยสองขั้นตอนหลัก คือ ขั้นตอนแรก การตั้งสมมติฐานจากปัญหาที่สนใจ และขั้นตอนที่สอง การทดสอบสมมติฐานเพื่อการตัดสินใจ สำหรับขั้นตอนแรก ผู้ใช้ข้อมูลจำเป็นที่จะต้องใช้ความรู้เฉพาะสาขา (Domain Knowledge) ที่เกี่ยวข้องกับปัญหาที่สนใจ เพื่อสร้างสมมติฐานมาประกอบเข้าด้วยกันกับโมเดลสถิติที่สมเหตุสมผล โดยคำนึงถึงปัญหาความสัมพันธ์ร่วมกันของข้อมูล (Endogeneity) ที่ได้เกริ่นไปแล้วในบทความของผู้เขียนในรอบก่อน และบทความเศรษฐสารนี้จะนำผู้อ่านทุกท่านมาทำความเข้าใจเกี่ยวกับขั้นตอนที่สอง การทดสอบสมมติฐาน ให้ลึกซึ้งเพื่อให้การตัดสินใจบนพื้นฐานข้อมูลแม่นยำและน่าเชื่อถือ

การทดสอบสมมติฐานคืออะไร

การทดสอบสมมติฐาน (Hypothesis Testing) เป็นขั้นตอนการวิเคราะห์ข้อมูลที่ดำเนินการหลังจากได้โมเดลสถิติที่สมเหตุสมสมผลแล้ว ขั้นตอนนี้เริ่มต้นด้วยการกำหนดสมมติฐานว่าง (Null Hypothesis) และ สมมติฐานแย้ง (Alternative Hypothesis) เช่น ในเชิงนโยบายเพื่อที่จะตอบคำถาม “ห้องเรียนที่มีขนาดเล็กช่วยส่งเสริมการเรียนรู้หรือไม่” สมมติฐานว่างระบุว่าขนาดห้องเรียนไม่มีผลต่อการเรียนรู้ ในขณะที่สมมติฐานแย้งบ่งชี้ในทางตรงข้าม (ขนาดห้องเรียนมีผลต่อการเรียนรู้)

ในเชิงธุรกิจ เพื่อที่จะตอบคำถามว่า “การลงทุนในบริษัทหนึ่งมีความเสี่ยงมากกว่าการลงทุนในดัชนีตลาดหรือไม่” สมมติฐานว่างระบุว่าการลงทุนเสี่ยงเท่ากับหรือน้อยกว่าดัชนีตลาด ในขณะที่สมมติฐานแย้งจะบอกว่าการลงทุนเสี่ยงกว่าดัชนีตลาด ถ้าผู้อ่านทำการทดลอง หรือ สุ่มเก็บตัวอย่างหลายรอบ แน่นอนว่าผลลัพธ์ทางสถิติในแต่ละรอบจะไม่ตรงกัน ดังนั้น ผู้อ่านจะต้องระบุเขตการปฏิเสธ (Rejection Region) หรือค่า p-value เพื่อตัดสินใจว่า จากข้อมูลที่ได้ เมื่อใดที่ผู้อ่านสามารถสรุปสมมติฐานแย้งได้ เมื่อกำหนดสมมติฐาน เขตการปฏิเสธ (หรือ ค่า p-value) และข้อมูลที่รวบรวมได้จากกลุ่มตัวอย่างแล้ว ผู้อ่านสามารถดำเนินการทดสอบสมมติฐานเพื่อที่จะได้ผลลัพธ์ทางสถิติสำหรับการตัดสินใจ (Stobierski, 2021) ดังสรุปในรูปที่ 1

รูปที่ 1 ขั้นตอนการทดสอบสมมติฐานสำหรับการตัดสินใจโดยใช้ข้อมูล

เพื่อให้การทดสอบสมมติฐานนั้นแม่นยำ ผู้อ่านต้องคำนวณหาค่าคลาดเคลื่อนมาตรฐาน (Standard Error) ให้ถูกต้อง ถ้าค่าคลาดเคลื่อนมาตรฐานต่ำกว่าที่ควรจะเป็น การตัดสินใจบนพื้นฐานข้อมูลจะผิดเพี้ยนไป กล่าวคือ ที่จริงแล้วสองตัวแปรนั้นไม่มีความสัมพันธ์ร่วมกัน แต่ผลสรุปจากการวิเคราะห์ข้อมูลกลับบอกว่าสองตัวแปรนั้นมีความสัมพันธ์ร่วมกัน เพื่อให้ผู้อ่านเข้าใจค่าคลาดเคลื่อนมาตรฐานซึ่งเป็นตัวเลขที่ชี้ชะตาสำหรับการตัดสินใจบนพื้นฐานข้อมูล ดังนั้น เริ่มต้น เราจำเป็นต้องเข้าใจปัญหาความแปรปรวนต่าง (Heteroskedasticity) และความสัมพันธ์อัตโนมัติ (Serial Correlation) ก่อน จึงจะสามารถเข้าใจขั้นตอนการทดสอบสมมติฐานได้

ปัญหาความแปรปรวนต่าง (Heteroskedasticity)

หากผู้อ่านต้องการตอบคำถามที่ว่า “ห้องเรียนที่มีขนาดเล็กช่วยส่งเสริมการเรียนรู้หรือไม่” ก่อนเปิดภาคเรียน ผู้อ่านได้สุ่มนักเรียนบางส่วนให้อยู่ในห้องเรียนขนาดเล็ก และนักเรียนส่วนที่เหลือให้อยู่ในห้องเรียนขนาดใหญ่ เมื่อครบภาคเรียน ผู้อ่านจึงแจกแบบทดสอบการวัดผลการเรียนรู้รายบุคคล ผลจากการวิเคราะห์ข้อมูลแสดงถึงความสัมพันธ์ของจำนวนนักเรียนต่อห้อง และคะแนนทดสอบรายบุคคล แสดงให้เห็นในรูปที่ 2

เพื่อที่จะตอบคำถามข้างต้น ผู้อ่านจะต้องคำนวณค่าคลาดเคลื่อนมาตรฐานเพื่อทดสอบสมมติฐาน ปัญหาที่สามารถพบได้ คือ ควรใช้ค่าคลาดเคลื่อนมาตรฐานที่มาจากความแปรปรวนร่วม (Homoskedasticity) ซึ่งเป็นค่าเริ่มต้นในโปรแกรมสถิติหรือไม่

จากรูปที่ 3 สังเกตได้ว่า ในห้องเรียนที่มีจำนวนนักเรียนมากกว่า คะแนนสอบรายบุคคลมีความแปรปรวนสูงกว่า แสดงให้เห็นถึงปัญหาความแปรปรวนที่ต่างกันของคะแนนสอบระหว่างนักเรียนที่เรียนในห้องเรียนขนาดใหญ่กับนักเรียนที่เรียนในห้องเรียนขนาดเล็ก หากผู้ใช้ข้อมูลไม่ได้คำนึงถึงปัญหานี้และเลือกคำนวณค่าคลาดเคลื่อนมาตรฐานโดยใช้สูตรทั่วไปที่สร้างอยู่บนสมมติฐานความแปรปรวนร่วม (Homoskedasticity) ค่าคลาดเคลื่อนมาตรฐานที่ผู้ใช้ข้อมูลได้ย่อมแตกต่างจากค่าที่แท้จริง ค่าคลาดเคลื่อนอาจมากหรือน้อยเกินไปขึ้นอยู่กับการกระจายความแปรปรวนในชุดข้อมูล

ดังนั้น การนำค่าคลาดเคลื่อนมาตรฐานที่ไม่ถูกต้องดังกล่าวไปใช้งาน อาจทำให้เกิดข้อสรุปที่ไม่สอดคล้องกับความเป็นจริง (Stock and Watson, 2020) เช่น แท้จริงแล้วขนาดห้องเรียนไม่ได้ส่งผลต่อการเรียนรู้ แต่การใช้สมมติฐานความแปรปรวนร่วมภายใต้สถานการณ์นี้กลับทำให้เกิดข้อสรุปว่า ห้องเรียนที่มีขนาดเล็กช่วยส่งเสริมการเรียนรู้

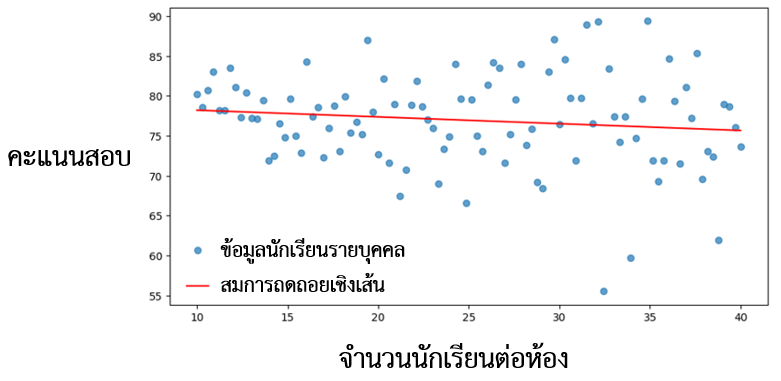
รูปที่ 2 แผนภูมิกระจายและสมการถดถอยเชิงเส้นสำหรับจำนวนนักเรียนต่อห้องและคะแนนสอบ

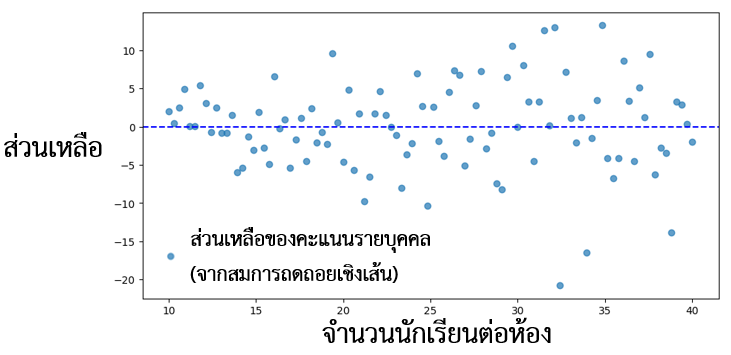
รูปที่ 3 แผนภูมิกระจายสำหรับส่วนเหลือจากสมการถดถอยเชิงเส้นและจำนวนนักเรียนต่อห้องที่มา: คำนวณโดยผู้เขียน

แนวทางการแก้ปัญหาความแปรปรวนต่างที่ได้รับความนิยม คือ การใช้สูตรคำนวณค่าคลาดเคลื่อนมาตรฐานที่ได้มีการปรับสูตรให้เหมาะสมกับข้อมูลที่มีความแปรปรวนต่าง เช่น Heteroskedasticity-Consistent Covariance Matrix Estimator โดย White (1980) จากรูปที่ 4 สังเกตได้ว่า ในกรณีที่ความแปรปรวนของคะแนนสอบรายบุคคลขึ้นอยู่กับขนาดห้องเรียน ค่าความคลาดเคลื่อนมาตรฐานที่ใช้สูตร White (1980) จะแตกต่างกับค่าความคลาดเคลื่อนที่ใช้สมมติฐานความแปรปรวนร่วม

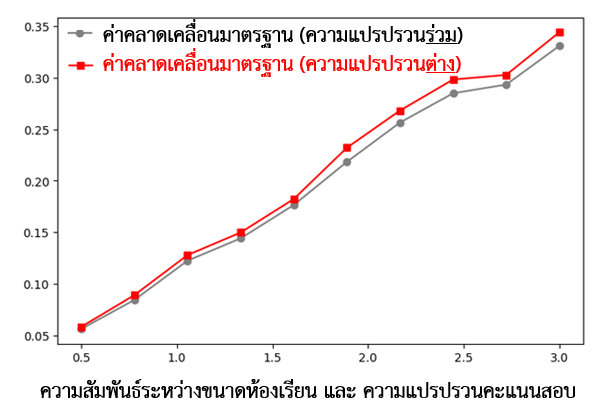
รูปที่ 4 กราฟเส้นเปรียบเทียบ Homoskedastic Standard Error และ Heteroskedastic Standard Error (White, 1980) ที่มา: คำนวณโดยผู้เขียน

สูตรของ White (1980) ได้รับการยอมรับและถูกนำไปใช้กันอย่างกว้างขวาง ทั้งงานวิจัยเชิงนโยบายและงานวิจัยเชิงธุรกิจ ตัวอย่างงานวิจัยเชิงนโยบาย เช่น งานของ Cheng et al. (2020) ที่ต้องการตอบคำถามว่า “การแพร่กระจายเทคโนโลยีสารสนเทศมีผลต่อการเติบโตทางเศรษฐกิจอย่างไร” เพื่อที่จะตอบคำถามนี้ Cheng et al. (2020) ได้กำหนดตัวแปรที่ส่งผลต่อการเติบโตทางเศรษฐกิจให้ประกอบด้วย ศักยภาพการใช้เทคโนโลยี วัฏจักรทางเศรษฐกิจ (Business cycle) และปัจจัยอื่นที่เกี่ยวข้อง

งานวิจัยพบว่าพฤติกรรมของตัวแปรในแต่ละประเทศมีความแตกต่างกัน ก่อให้เกิดปัญหาความแปรปรวนต่าง กล่าวคือ ความแปรปรวนของตัวแปรในแต่ละประเทศแตกต่างกัน เช่น ในกลุ่มประเทศที่มีเสถียรภาพทางเศรษฐกิจ การใช้เทคโนโลยีอาจจะมีความหลากหลายกว่า ทำให้ความแปรปรวนจากผลกระทบของเทคโนโลยีที่มีต่อระบบเศรษฐกิจอาจจะสูงกว่า เป็นต้น งานวิจัยจึงได้ใช้สูตรของ White (1980) แทนที่จะใช้สูตรการคำนวณค่าคลาดเคลื่อนมาตรฐานทั่วไปที่อยู่บนสมมติฐานความแปรปรวนร่วม หลังจากปรับสูตรคำนวณค่าคลาดเคลื่อนมาตรฐานให้เหมาะสมแล้ว งานวิจัยจึงสามารถสรุปผลยืนยันว่า การแพร่กระจายเทคโนโลยีสารสนเทศส่งผลดีต่อการเติบโตทางเศรษฐกิจ

ตัวอย่างงานวิจัยในเชิงธุรกิจ เช่น Liu et al. (2019) ที่ใช้สูตร White (1980) ในการวิเคราะห์ผลของปัจจัยคุณค่า (Value Factor) ต่อผลตอบแทนทางการเงินของบริษัทจีน นอกจากสูตรของ White (1980) ยังมีแนวทางอื่นที่ใช้แก้ปัญหาความแปรปรวนต่าง ได้แก่ Weighted Least Squares (WLS) หรือ Generalized Least Squares (GLS) เป็นต้น (Stock and Watson, 2020) ซึ่งแต่ละวิธีมีข้อดีข้อเสียแตกต่างกันออกไป การเลือกใช้สูตรการคำนวณเพื่อแก้ปัญหาความแปรปรวนต่างจะขึ้นอยู่กับคุณลักษณะของข้อมูลที่เรามี เช่น ขนาดของกลุ่มตัวอย่าง (sample size), พฤติกรรมของค่าคลาดเคลื่อน (error term) รวมไปถึงสิ่งที่เราทราบและไม่ทราบเกี่ยวกับค่าคลาดเคลื่อน

นอกจากปัญหาความแปรปรวนต่างแล้ว ปัญหาสถิติที่สามารถเกิดขึ้นได้สำหรับข้อมูลภาคตัดขวาง (Cross-Sectional Data) หรือ ข้อมูลแผง (Panel Data) คือ ปัญหาการรวมกันเป็นกลุ่ม (Clustering) ซึ่งเกิดขึ้นเมื่อผู้ใช้ข้อมูลต้องการศึกษาผลกระทบของปัจจัยร่วมที่มีต่อผลลัพธ์แต่ละบุคคล และ แนวทางแก้ปัญหาแนวทางหนึ่งที่ได้รับความนิยม คือ การประมาณค่าคลาดเคลื่อนมาตรฐานอิงกลุ่ม (Clustered Standard Error) ซึ่งเป็นวิธีที่นิยมใช้ในงานวิจัยเชิงนโยบายและธุรกิจ เช่น งานของ Angrist and Lavy (2009) ที่ต้องการตอบคำถามว่า “แรงจูงใจตัวเงินมีผลต่ออัตราการสอบผ่านมัธยมปลายในประเทศอิสราเอลหรือไม่” โดย Angrist and Lavy (2009) ศึกษาวิธีการทดลองแบบสุ่ม (Randomized Controlled Trial) ที่เกิดขึ้นในระดับโรงเรียน เช่น โรงเรียนบางส่วนให้รางวัลเป็นเงินสำหรับนักเรียนที่สอบผ่าน และ โรงเรียนที่เหลือไม่ได้ใช้นโยบายนี้

ดังนั้น นักเรียนที่อยู่ในโรงเรียนเดียวกันย่อมได้รับอิทธิพลจากแรงจูงใจในลักษณะเดียวกัน แสดงให้เห็นถึงปัญหาการรวมกันเป็นกลุ่ม ส่งผลให้ค่าคลาดเคลื่อนมาตรฐานที่คิดจากความแปรปรวนร่วมซึ่งเป็นค่าเริ่มต้นของโปรแกรมสถิตินั้นต่ำกว่าที่ควรจะเป็น หลังจากที่ปรับสูตรคำนวณค่าคลาดเคลื่อนมาตรฐานให้สอดคล้องกับปัญหาการรวมกันเป็นกลุ่มแล้ว

งานวิจัยได้ข้อสรุปว่า แรงจูงใจตัวเงินมีผลต่อการสอบผ่านมัธยมปลายในกลุ่มนักเรียนหญิง แต่ไม่พบความแตกต่างของอัตราการสอบผ่านมัธยมปลายในกลุ่มนักเรียนชาย นอกจากนี้ ปัญหาการรวมกันเป็นกลุ่มสามารถพบได้ในการศึกษาอื่น เช่น การศึกษาผลกระทบของมลพิษทางอากาศต่อประสิทธิภาพแรงงานโดย Fu et al. (2021) และ การศึกษาผลกระทบของหุ่นยนต์ต่อแรงงานในระบบเศรษฐกิจโดย Autor and Salomons (2018) เป็นต้น

ปัญหาความสัมพันธ์อัตโนมัติ (Serial Correlation)

หากผู้อ่านต้องการตอบคำถามที่ว่า “การลงทุนในสินทรัพย์หนึ่งมีความเสี่ยงเท่าใด” ผู้อ่านสามารถเลือกใช้แบบจำลองกำหนดราคาสินทรัพย์ เช่น Capital Asset Pricing Model (CAPM) (Fama and French, 2004) เพื่อคำนวณค่า Beta ที่แสดงถึงความเสี่ยงของผลตอบแทนโดยใช้สมการถดถอยเชิงเส้น ถ้าสมการแสดงค่า Beta ที่สูง (ความชันของสมการถดถอยเชิงเส้นสูง) การลงทุนนั้นย่อมมีความเสี่ยงสูง ถ้าดัชนีตลาดเป็นขาขึ้น ราคาสินทรัพย์นั้นย่อมสูงอย่างน่าตกใจ แต่ในกรณีที่ดัชนีตลาดเป็นขาลง ราคาสินทรัพย์นั้นสามารถตกลงอย่างน่าตกใจได้เช่นเดียวกัน

ผลลัพธ์จากการวิเคราะห์ข้อมูลแสดงในรูปที่ 5 และ รูปที่ 6 แสดงให้เห็นว่าผลตอบแทนของสินทรัพย์นั้นไม่แน่นอน สะท้อนให้เห็นถึงความเสี่ยงจากการลงทุน ดังนั้น ผู้อ่านต้องการทดสอบสมมติฐานว่า “การลงทุนในสินทรัพย์นั้นมีความเสี่ยงมากกว่าดัชนีตลาดหรือไม่” (ความชันของสมการถดถอยเชิงเส้นมากกว่า 1 หรือไม่) และคำนวณค่าคลาดเคลื่อนมาตรฐานเพื่อทดสอบสมมติฐานดังกล่าว

จากที่กล่าวไปข้างต้น ปัญหาความแปรปรวนต่างเกิดขึ้นเมื่อคะแนนสอบของนักเรียนมีความแปรปรวนที่ต่างกันระหว่างห้องเรียนขนาดเล็กและห้องเรียนขนาดใหญ่ ปัญหาการรวมกันเป็นกลุ่มเกิดขึ้นเมื่อนักเรียนที่อยู่ในโรงเรียนเดียวกันได้รับอิทธิพลจากแรงจูงใจเช่นเดียวกัน ปัญหาเหล่านี้มักจะเกิดขึ้นในข้อมูลภาคตัดขวางหรือ ข้อมูลแผง แต่ข้อมูลที่ใช้ตอบคำถามนี้เป็นข้อมูลอนุกรมเวลา (Time-Series Data)

ดังนั้น ปัญหาที่พบ คือ ปัญหาความสัมพันธ์อัตโนมัติ (Serial Correlation) รูปที่ 7 แสดงให้เห็นว่า ผลตอบแทนของสินทรัพย์นั้นมีความสัมพันธ์อัตโนมัติเป็นบวก กล่าวคือ ถ้าผลตอบแทนในช่วงเวลาก่อนหน้าสูงกว่าค่าเฉลี่ย มีความเป็นไปได้ที่ผลตอบแทนในช่วงเวลาถัดมาจะสูงกว่าค่าเฉลี่ย เมื่อคำนวณจากผลตอบแทนที่เกิดขึ้นในอดีต เช่นเดียวกัน หากผู้ใช้ข้อมูลละเลยข้อสังเกตนี้และใช้ค่าคลาดเคลื่อนมาตรฐานโดยใช้สูตรทั่วไปที่สร้างอยู่บนสมมติฐานความแปรปรวนร่วม ค่าคลาดเคลื่อนมาตรฐานที่ได้ย่อมแตกต่างจากเดิมอย่างมาก อาจทำให้เกิดข้อสรุปที่ไม่สอดคล้องกับความเป็นจริง (Angrist and Pischke, 2009) เช่น แท้จริงแล้วการลงทุนในสินทรัพย์นี้มีความเสี่ยงใกล้เคียงกับดัชนีตลาด แต่ข้อสรุปทางสถิติกลับบ่งชี้ว่ามีความเสี่ยงสูงกว่าดัชนีตลาดอย่างมีนัยยะสำคัญ

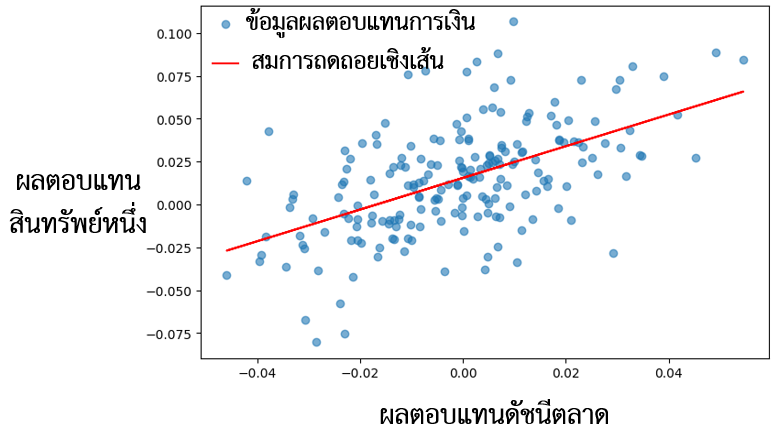
รูปที่ 4.1 แผนภูมิกระจายและสมการถดถอยเชิงเส้นสำหรับผลตอบแทนโดยใช้สมการ CAPM

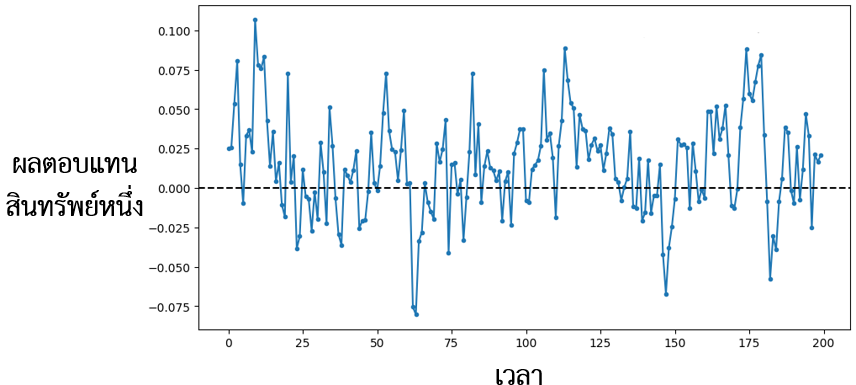
รูปที่ 4.2 กราฟเส้นของผลตอบแทนสินทรัพย์หนึ่งในช่วงเวลาหนึ่ง

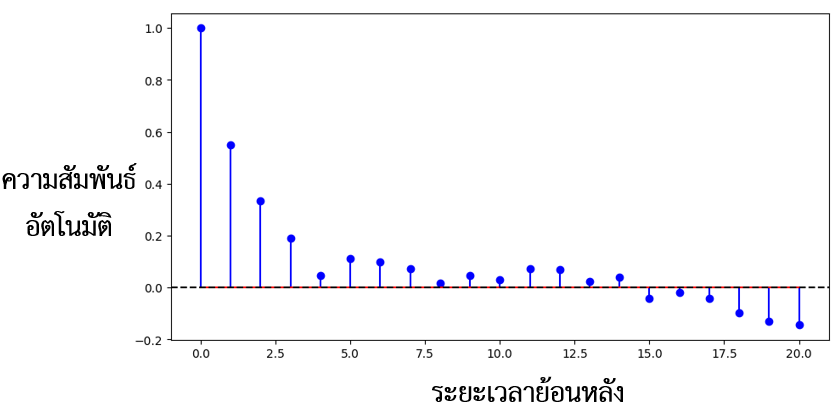
รูปที่ 4.3 ความสัมพันธ์อัตโนมัติของสินทรัพย์หนึ่ง ที่มา: คำนวณโดยผู้เขียน

แนวทางการแก้ปัญหาความสัมพันธ์อัตโนมัติที่ได้รับความนิยม คือ การใช้สูตรคำนวณค่าคลาดเคลื่อนมาตรฐานที่ได้มีการปรับสูตรให้เหมาะสมกับข้อมูลที่มีความสัมพันธ์อัตโนมัติ เช่น Heteroskedasticity and Autocorrelation Consistent (HAC) Covariance Matrix Estimator โดย Newey and West (1987) จากรูปที่ 5 สังเกตได้ว่า ในกรณีที่เกิดปัญหาความสัมพันธ์อัตโนมัติ ค่าความคลาดเคลื่อนมาตรฐานที่ใช้สูตร Newey and West (1987) จะแตกต่างกับค่าความคลาดเคลื่อนที่ใช้สมมติฐานความแปรปรวนร่วม โดยเฉพาะอย่างยิ่ง เมื่อความสัมพันธ์อัตโนมัติมีค่ามาก

นอกจากนี้ Bertrand et al. (2004) ยังชี้ให้เห็นว่า ปัญหาความสัมพันธ์อัตโนมัติสามารถเกิดขึ้นได้กับการประมาณค่า Difference-in-Difference ส่งผลให้ค่าคลาดเคลื่อนมาตรฐานต่ำกว่าที่ควรจะเป็น และการละเลยปัญหานี้ส่งผลให้ผู้ใช้ข้อมูลสรุปสมมติฐานแย้งบ่อยกว่าที่ควรจะเป็น (Petersen, 2008)

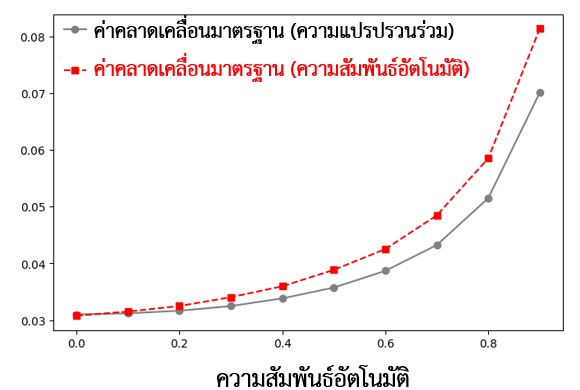
รูปที่ 8 Homoskedastic Standard Error และ Newey and West (1987) Standard Error ที่มา: คำนวณโดยผู้เขียน

สูตรของ Newey and West (1987) ได้รับการยอมรับและถูกนำไปใช้กันอย่างกว้างขวาง ตัวอย่างงานวิจัยเชิงนโยบายและธุรกิจ เช่น งานของ Ardia et al. (2023) ที่ต้องการตอบคำถามว่า “ความกังวลเกี่ยวกับการเปลี่ยนแปลงสภาพภูมิอากาศมีผลต่อผลตอบแทนในหุ้นบริษัทหรือไม่” เพื่อที่จะตอบคำถามนี้ Ardia et al. (2023) ได้คำนวณอนุกรมเวลาที่แสดงถึงผลตอบแทนค่าเฉลี่ยถ่วงน้ำหนักของหุ้นกลุ่มที่เป็นมิตรต่อสิ่งแวดล้อม และอนุกรมเวลาที่แสดงถึงผลตอบแทนของหุ้นกลุ่มที่ไม่เป็นมิตรต่อสิ่งแวดล้อม

เช่นเดียวกับตัวอย่างข้างต้น ผลตอบแทนในรูปแบบอนุกรมเวลาสามารถเกิดปัญหาความสัมพันธ์อัตโนมัติได้ ดังนั้น งานวิจัยได้ใช้สูตรของ Newey and West (1987) แทนที่จะใช้สูตรการคำนวณค่าคลาดเคลื่อนมาตรฐานทั่วไปที่อยู่บนสมมติฐานความแปรปรวนร่วม หลังจากปรับสูตรคำนวณค่าคลาดเคลื่อนมาตรฐานให้เหมาะสมแล้ว งานวิจัยสามารถยืนยันได้ว่า ความกังวลเกี่ยวกับการเปลี่ยนแปลงสภาพภูมิอากาศทำให้ราคาของหุ้นที่เป็นมิตรต่อสิ่งแวดล้อมสูงขึ้น ในขณะเดียวกัน ราคาของหุ้นที่ไม่เป็นมิตรต่อสิ่งแวดล้อมจะลดลง

นอกจากนี้ Liu et al. (2019) ใช้สมการ Fama-MacBeth ศึกษาปัจจัยมูลค่าที่มีต่ออนุกรมเวลาหุ้นรายตัวในตลาดหลักทรัพย์ประเทศจีน เนื่องจากผลตอบแทนในรูปแบบอนุกรมเวลาสามารถเกิดปัญหาความสัมพันธ์อัตโนมัติ งานวิจัยได้ใช้สูตร Newey and West (1987) เพื่อยืนยันว่าปัจจัยร่วมที่แสดงถึงมูลค่าบริษัท (Value Factor) สามารถอธิบายผลตอบแทนหุ้นรายตัวในตลาดหลักทรัพย์ประเทศจีนได้ดี

บทสรุป

การตัดสินใจบนพื้นฐานข้อมูลเป็นทักษะที่สำคัญในยุคนี้ ประกอบด้วยสองขั้นตอนหลัก คือ ขั้นตอนแรก การตั้งสมมติฐานจากปัญหาที่สนใจ และขั้นตอนที่สอง การทดสอบสมมติฐานเพื่อตัดสินใจ ดังนั้น ค่าคลาดเคลื่อนมาตรฐานจึงเป็นตัวเลขที่สำคัญสำหรับการตัดสินใจว่า ตัวแปรต้นส่งผลต่อตัวแปรตามหรือไม่ เช่น “ห้องเรียนที่มีขนาดเล็กช่วยส่งเสริมการเรียนรู้หรือไม่” และ “การลงทุนในบริษัทหนึ่งมีความเสี่ยงมากกว่าการลงทุนในดัชนีตลาดหรือไม่” เป็นต้น ดังนั้น ผู้ใช้ข้อมูลอย่างน้อยต้องตระหนักถึงปัญหาความแปรปรวนต่าง (Heteroskedasticity) และความสัมพันธ์อัตโนมัติ (Serial Correlation) ในการศึกษาแต่ละครั้ง เพื่อหลีกเลี่ยงการตัดสินใจทางสถิติที่ผิดพลาดไปได้

นอกจากนั้น ผู้ใช้ข้อมูลจำเป็นต้องใช้โมเดลสถิติที่สมเหตุสมผลด้วยเช่นเดียวกัน เช่น การตั้งสมมติฐานให้สอดคล้องกับปัญหาที่สนใจ การเลือกตัวแปรที่ใช้ในโมเดล รวมไปถึงการวิเคราะห์ว่าผลลัพธ์ที่ได้สมเหตุสมผลหรือไม่ เป็นต้น ผู้อ่านจะสังเกตได้ว่าคำถามเหล่านี้ไม่ใช่คำถามสถิติ แต่เป็นคำถามที่ต้องใช้ความรู้เฉพาะทาง เนื่องจาก วิชาสถิติสอนการวิเคราะห์ข้อมูลบนพื้นฐานโมเดลที่สมเหตุสมผล แต่ไม่ได้ระบุว่าโมเดลที่สมเหตุสมผลควรเป็นอย่างไร ดังนั้น เพื่อให้มั่นใจว่าผลสรุปจากการวิเคราะห์ข้อมูลนั้นสามารถนำไปใช้ในสถานการณ์จริงได้ ผู้ใช้ข้อมูลจำเป็นต้องเข้าใจทั้งลักษณะข้อมูลและทฤษฎีเศรษฐศาสตร์อย่างถ่องแท้

Acknowledgement: ผู้เขียนขอขอบคุณ ดร.ษิฌา ทับทิมพรรณ์ สำหรับข้อเสนอแนะในการเขียนบทความนี้ให้อ่านง่ายยิ่งขึ้น

เอกสารอ้างอิง

Angrist, J. D., & Pischke, J. S. (2009). Mostly harmless econometrics: An empiricist's companion. Princeton university press.

Angrist, J., & Lavy, V. (2009). The effects of high stakes high school achievement awards: Evidence from a randomized trial. American economic review, 99(4), 1384-1414.

Ardia, D., Bluteau, K., Boudt, K., & Inghelbrecht, K. (2023). Climate change concerns and the performance of green vs. brown stocks. Management Science, 69(12), 7607-7632.

Autor, D., & Salomons, A. (2018). Is automation labor-displacing? Productivity growth, employment, and the labor share (No. w24871). National Bureau of Economic Research.

Bertrand, M., Duflo, E., & Mullainathan, S. (2004). How much should we trust differences-in-differences estimates?. The Quarterly journal of economics, 119(1), 249-275.

Cheng, C. Y., Chien, M. S., & Lee, C. C. (2021). ICT diffusion, financial development, and economic growth: An international cross-country analysis. Economic modelling, 94, 662-671.

Fama, E. F., & French, K. R. (2004). The capital asset pricing model: Theory and evidence. Journal of economic perspectives, 18(3), 25-46.

Fu, S., Viard, V. B., & Zhang, P. (2021). Air pollution and manufacturing firm productivity: Nationwide estimates for China. The Economic Journal, 131(640), 3241-3273.

Kihn, M. (2025, Jan 2). 8 Mega-Trends That Matter For Marketing In 2025. Forbes. https://www.forbes.com/councils/forbescommunicationscouncil/2025/01/02/8-mega-trends-that-matter-for-marketing-in-2025/

Liu, J., Stambaugh, R. F., & Yuan, Y. (2019). Size and value in China. Journal of financial economics, 134(1), 48-69.

Newey, W. K., & West, K. D. (1987). Hypothesis testing with efficient method of moments estimation. International Economic Review, 777-787.

Petersen, M. A. (2008). Estimating standard errors in finance panel data sets: Comparing approaches. The Review of financial studies, 22(1), 435-480.

Sargent, T. J. (1976). The observational equivalence of natural and unnatural rate theories of macroeconomics. Journal of Political Economy, 84(3), 631-640.

Stobierski T. (2021, Mar 30). A Beginner’s Guide to Hypothesis Testing in Business. Harvard Business School Online. https://online.hbs.edu/blog/post/hypothesis-testing

Stock, J. H., & Watson, M. W. (2020). Introduction to econometrics. Pearson.

Tableau. (n.d.). A Guide To Data Driven Decision Making: What It Is, Its Importance, & How To Implement It. https://www.tableau.com/learn/articles/data-driven-decision-making

White, H. (1980). A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica: journal of the Econometric Society, 817-838.

สำนักงานพัฒนาวิทยาศาสตร์และเทคโนโลยีแห่งชาติ. (2020). Megatrends 2020 – 2030 สิ่งที่มีความหมายต่อคุณ ธุรกิจและการเติบโตของนวัตกรรม. https://www.nstda.or.th/home/knowledge_post/megatrend-2020-2030/