ในยุคที่ข้อมูลอยู่รอบตัวเรา การตัดสินใจโดยใช้ข้อมูลให้เป็นประโยชน์ (Data-Driven Decision Making) ดีกว่าการตัดสินใจโดยใช้สัญชาตญาณเพียงอย่างเดียว จากการสำรวจของ NewVantage Partners พบว่า ร้อยละ 98 ของผู้บริหารกลุ่มตัวอย่างต้องการสร้างให้บริษัทมีวัฒนธรรมแบบขับเคลื่อนด้วยข้อมูล (Data-Driven Culture) แสดงถึงความนิยมของการพยายามตัดสินใจด้วยความรอบรู้โดยอาศัยข้อมูลแทนการคาดเดา และผลสำรวจจาก Tableau, n.d. และ Tabrizi et al., 2019 พบว่า ผู้บริหารจำนวนแค่น้อยกว่า 1 ใน 3 เชื่อว่าจะประสบความสำเร็จได้จากการให้ความสำคัญกับการลงทุนด้านเทคโนโลยีโดยไม่จำเป็นต้องสร้างวัฒนธรรมองค์กร

ดังนั้น การนำข้อมูลมาใช้และใช้อย่างถูกต้องจึงเป็นทักษะที่สำคัญสำหรับทุกคนและในทุกระดับการตัดสินใจ เพื่อบรรลุเป้าหมายนี้ ผู้ใช้ข้อมูลควรตระหนักถึงปัญหาทางสถิติที่อาจเกิดขึ้นได้ในทุกมิติ บทความนี้จะนำเสนอเรื่องปัญหาความสัมพันธ์ร่วมกันของข้อมูล (Endogeneity) ซึ่งเป็นปัญหาหนึ่งที่ผู้คนทั่วไปมักจะมองข้าม ส่งผลให้เกิดความผิดพลาดในการวิเคราะห์ข้อมูล

ตัวอย่างคำถามที่ใช้ข้อมูลตัดสินใจ อาทิ นโยบายการศึกษาภาคบังคับช่วยยกระดับค่าจ้างหรือไม่, การเพิ่มกำลังตำรวจในพื้นที่ช่วยลดจำนวนอาชญากรรมหรือไม่, โฆษณาช่วยเพิ่มยอดขายหรือไม่, ควรลงทุนใน กองทุนเชิงรุก (Active Fund) หรือ กองทุนเชิงรับ (Passive Fund) ดีกว่ากัน ถึงแม้คำถามเหล่านี้ดูเหมือนไม่เกี่ยวข้องกัน แต่การตอบคำถามเหล่านี้โดยใช้ข้อมูลจำเป็นต้องตระหนักถึงปัญหาความสัมพันธ์ร่วมกันของข้อมูลทั้งสิ้น มิเช่นนั้น ผลลัพธ์สถิติที่ได้จะสูงหรือต่ำกว่าความเป็นจริง ทำให้ตัดสินใจผิดพลาดได้

ยกตัวอย่าง เราอาจพบว่านักเรียนที่สามารถเรียนรู้ได้ดีกว่ามีแนวโน้มเรียนต่อที่สูงกว่า และถ้าเปรียบเทียบนักเรียนกลุ่มที่ศึกษาต่อและกลุ่มที่เลือกไม่ศึกษาต่อแล้ว กลุ่มแรกย่อมได้รับค่าจ้างที่สูงกว่าเพราะการมีความสามารถในการเรียนรู้แต่เดิมที่ดีกว่า (Angrist and Krueger, 1991) เราจึงไม่สามารถสรุปได้ว่า “การศึกษาที่เพิ่มขึ้นทำให้ค่าจ้างที่ได้รับสูงขึ้น” เพราะ ความสามารถในการเรียนรู้ที่มีอยู่เดิมเป็นผลจากปัจจัยอื่นซึ่งอาจเป็นส่วนสำคัญหลักที่ทำให้ได้รับค่าจ้างที่สูงขึ้น ไม่ใช่ระดับการศึกษา

ในเชิงนโยบาย อาจมีตัวเลือกอื่นที่คุ้มค่ากว่าการเพิ่มระดับการศึกษาภาคบังคับให้สูงขึ้น เช่น การยกระดับชีวิตของประชาชนในมิติอื่น ๆ เช่น มิติด้านสุขภาพ ที่ช่วยยกระดับความสามารถในการเรียนรู้อาจมีประสิทธิภาพมากกว่า เป็นต้น อีกหนึ่งตัวอย่าง หากผู้บริหารกำลังตัดสินใจว่าควรทุ่มงบโฆษณาเพื่อเพิ่มยอดขายหรือไม่ การเปรียบเทียบยอดขายที่มาจากกลุ่มลูกค้าที่เห็นโฆษณาบริษัทและกลุ่มลูกค้าที่ไม่เห็นโฆษณาทำให้บริษัทตัดสินใจผิดพลาดได้ (Zantedeschi et al., 2017) เนื่องจากลูกค้ากลุ่มแรกอาจชื่นชอบสินค้าของบริษัทเป็นพิเศษ ยอดขายของลูกค้ากลุ่มแรกจึงสูงกว่าลูกค้ากลุ่มหลัง ถ้าบริษัทไม่ตระหนักถึงปัญหานี้ อาจจะต้องทุ่มงบโฆษณาทั้ง ๆ ที่โฆษณานั้นอาจไม่ได้ส่งผลกับยอดขาย

ปัญหาเศรษฐมิติที่กล่าวมาข้างต้น คือ ปัญหาความสัมพันธ์ร่วมกันของข้อมูลที่ทำให้ผลลัพธ์ทางสถิติไม่ได้สะท้อนความสัมพันธ์ที่แท้จริง ส่งผลให้เกิดความผิดพลาดในการนำผลวิเคราะห์ข้อมูลไปใช้สำหรับการตัดสินใจ ปัญหาความสัมพันธ์ร่วมกันของข้อมูลนี้เป็นปัญหาที่ถูกกล่าวถึงอยู่เสมอมาตั้งแต่ช่วงปี 1960

บทความวิชาการที่มีชื่อเสียงของ DePrano and Mayer (1965) ได้ชี้ให้เห็นว่าปัญหาความสัมพันธ์ร่วมกันของข้อมูลอาจส่งผลเชิงลบต่อความน่าเชื่อถือของการใช้สมการเซนต์หลุยส์ (St. Louis Equation) เพื่อประเมินความสำคัญของนโยบายการเงินและการคลังต่อกิจกรรมทางเศรษฐกิจ การวิจารณ์ของ DePrano and Mayer (1965) ทำให้เกิดความกังวลต่อข้อจำกัดของสมการเซนต์หลุยส์ (St. Louis Equation) ซึ่งมีอิทธิพลต่อการดำเนินนโยบายการเงินการคลังในสมัยนั้น เพื่อให้เข้าใจปัญหาความสัมพันธ์ร่วมกันของข้อมูล (Endogeneity) มากขึ้น บทความนี้จะพาเจาะลึกถึง ความหมาย ความสำคัญ และเสนอแนะแนวทางการแก้ปัญหา ดังนี้

เจาะลึกปัญหาความสัมพันธ์ร่วมกันของข้อมูล (Endogeneity)

ตัวอย่างแรก “นโยบายการศึกษาภาคบังคับช่วยยกระดับค่าจ้างหรือไม่” ดัดแปลงจาก Angrist and Krueger (1991) แรงจูงใจสำคัญของนโยบายนี้คือการยกระดับชีวิตของประชาชนให้มีรายได้ที่เหมาะสม เรามักจะตั้งคำถามว่า การศึกษาในระดับที่สูงขึ้นมีผลต่อค่าจ้างอย่างไร ถ้าเปรียบเทียบนักเรียนกลุ่มที่ศึกษาต่อและกลุ่มที่เลือกไม่ศึกษาต่อ เรามักพบว่านักเรียนกลุ่มแรกได้ค่าจ้างที่สูงกว่าโดยเฉลี่ย แต่ยังสรุปไม่ได้ว่า “การศึกษาที่สูงขึ้นทำให้ค่าจ้างเพิ่มขึ้น” เนื่องจาก Angrist and Pischke (2009) ได้ชี้ให้เห็นปัญหาว่า นักเรียนกลุ่มแรกแต่เดิมมีความสามารถในการเรียนรู้ที่ดีกว่าซึ่งมาจากปัจจัยอื่น โดยความสามารถที่ดีกว่าส่งผลให้นักเรียนกลุ่มแรกมีแนวโน้มเรียนต่อในระดับที่สูงขึ้น

ดังนั้น ถ้าไม่ระวังปัญหานี้ เราจะคำนวณได้ผลตอบแทนด้านการศึกษา (Returns to Education) ที่สูงกว่าความเป็นจริง ปัญหาลักษณะนี้ เรียกว่า Omitted Variable Bias หรือ อคติเกิดจากการละทิ้งตัวแปรสำคัญที่เกี่ยวข้องกับการศึกษาออกไป กล่าวคือ นอกเหนือจากระดับการศึกษาแล้ว ความสามารถแต่เดิมเป็นอีกหนึ่งตัวแปรสำคัญที่ส่งผลต่อการตัดสินใจศึกษาต่อและมีผลกระทบต่อค่าจ้างที่ได้รับ สรุปให้เห็นภาพยิ่งขึ้นในรูปแบบกราฟอวัฎจักรระบุทิศทาง (Directed Acyclic Graph) (Cuningham, 2021) ในรูปที่ 1

รูปที่ 1 ปัญหาความสัมพันธ์ร่วมกันของข้อมูล (Endogeneity) ในกรณี “นโยบายการศึกษาภาคบังคับช่วยยกระดับค่าจ้างหรือไม่”

หากผู้ใช้ข้อมูลไม่ได้ตระหนักถึงปัญหา Omitted Variable Bias ผู้ใช้ข้อมูลจะไม่ได้นำตัวแปรควบคุม (ความสามารถแต่เดิม) ที่ส่งผลต่อตัวแปรต้น (ระดับการศึกษา) และ ตัวแปรตาม (ค่าจ้าง) เข้ามาพิจารณาอย่างครบถ้วน ผลลัพธ์ทางสถิติที่ได้จะสูงหรือต่ำกว่าความเป็นจริง สำหรับตัวอย่างนี้ การไม่ได้นำความสามารถแต่เดิมมาพิจารณาจะทำให้ผลตอบแทนด้านการศึกษาที่ได้นั้นสูงกว่าความเป็นจริง เพราะผลตอบแทนด้านการศึกษาบางส่วนที่มาจากความสามารถแต่เดิมถูกนับรวมเข้าไปด้วย (Angrist and Pischke, 2009) รูปที่ 2 แสดงให้เห็นถึงผลลัพธ์ทางสถิติที่เกิดจากปัญหา Omitted Variable Bias

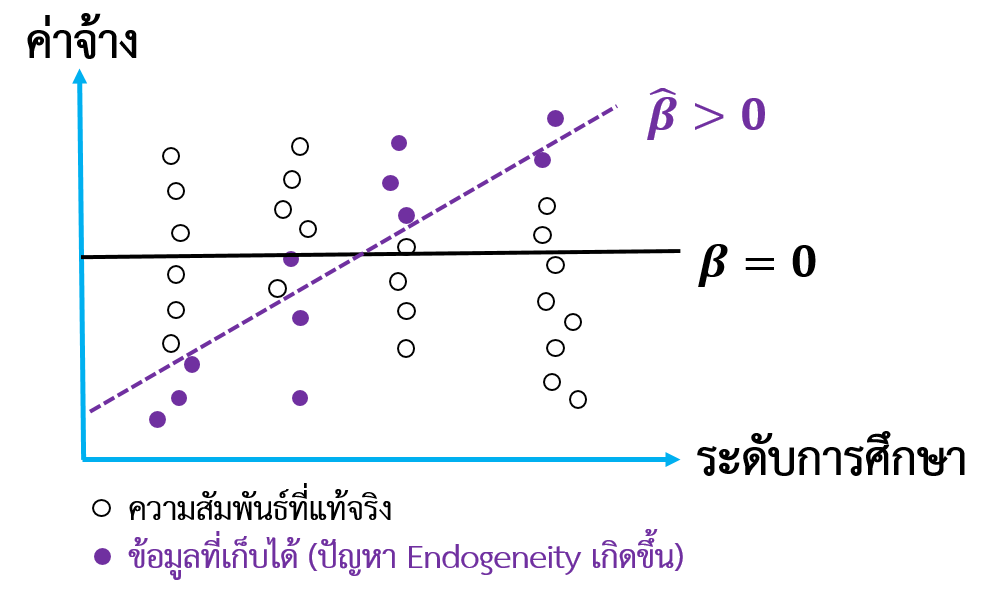
รูปที่ 2 ปัญหา Omitted Variable Bias สำหรับตัวอย่าง “นโยบายการศึกษาภาคบังคับช่วยยกระดับค่าจ้างหรือไม่”

อีกหนึ่งตัวอย่าง “การเพิ่มกำลังตำรวจในพื้นที่ช่วยลดจำนวนอาชญากรรมหรือไม่” ดัดแปลงจาก Di Tella and Schargrodsky (2004) และ Levitt and Snyder (1997) หากเราเปรียบเทียบจำนวนอาชญากรรมในสองพื้นที่โดยพื้นที่แรกมีจำนวนตำรวจมากกว่า เรามักพบว่าพื้นที่แรกกลับมีจำนวนอาชญากรรมสูงกว่า ถ้าไม่ระวังปัญหาความสัมพันธ์ร่วมกันของข้อมูล อาจเกิดข้อสรุปที่ผิดพลาดว่า “ตำรวจที่เพิ่มขึ้นทำให้อาชญากรรมในพื้นที่สูงขึ้น” เนื่องจาก พื้นที่ที่มีจำนวนอาชญากรรมสูงแต่เดิม จำเป็นต้องจ้างตำรวจในพื้นที่มากเพื่อจะได้ระงับเหตุได้ทันท่วงที

ถ้าพื้นที่แรกมีจำนวนอาชญากรรมที่สูงแต่เดิม ถึงแม้การเพิ่มกำลังตำรวจช่วยระงับอาชญากรรมได้ จำนวนอาชญากรรมที่ลดลงนั้นยังสูงกว่าพื้นที่อื่นอยู่ดี ปัญหาลักษณะนี้เรียกว่า Reverse Causality ที่เกิดขึ้นเมื่อข้อมูลมีความสัมพันธ์ที่ส่งผลซึ่งกันและกัน ข้อสรุปจากการวิเคราะห์ข้อมูลจึงอาจจะเกิดจากการสลับกันของสาเหตุผละผลลัพธ์ เรียกอีกอย่างว่า ปัญหาความเป็นไปได้ที่ตัวแปรตามส่งผลต่อตัวแปรต้น Simultaneity Bias ดังแสดงในรูปที่ 3

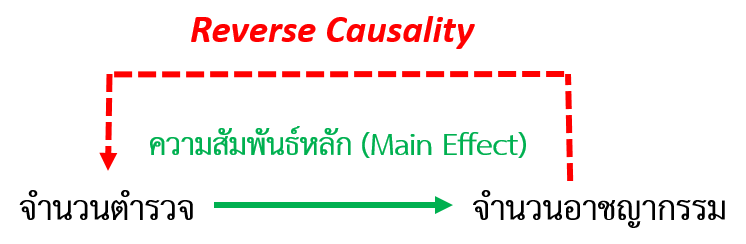
รูปที่ 3 ปัญหาความสัมพันธ์ร่วมกันของข้อมูล (Endogeneity) สำหรับตัวอย่าง “การเพิ่มกำลังตำรวจในพื้นที่ช่วยลดจำนวนอาชญากรรมหรือไม่”

หากผู้ใช้ข้อมูลไม่ได้ตระหนักถึงปัญหา Reverse Causality หรือ Simultaneity Bias กล่าวคือ ไม่ได้นำการกระจายกำลังตำรวจที่ขึ้นอยู่กับจำนวนอาชญากรรมเข้ามาพิจารณาอย่างรอบด้าน ความสัมพันธ์ทางสถิติที่ได้จะตรงข้ามกับความเป็นจริง Di Tella and Schargrodsky (2004) และ Levitt and Snyder (1997) ชี้ให้เห็นถึงปัญหานี้ว่า แม้ความจริงแล้ว ความสัมพันธ์หลักบ่งบอกว่าการระงับเหตุอาชญากรรมจากการเพิ่มกำลังตรวจนั้นได้ผล แต่ถ้าไม่ได้พิจารณาถึง Reverse Causality กล่าวคือ การกระจายกำลังตำรวจที่ขึ้นอยู่กับจำนวนอาชญากรรมในพื้นที่แต่เดิม ผลลัพธ์ทางสถิติจะบอกว่านโยบายนี้ไม่ได้ผล ทำให้จำนวนตำรวจมากกลายไปเป็นสาเหตุของการมีจำนวนอาชญากรรมสูง (ดังแสดงในรูปที่ 4) ส่งผลให้เกิดความผิดพลาดในการดำเนินนโยบายได้

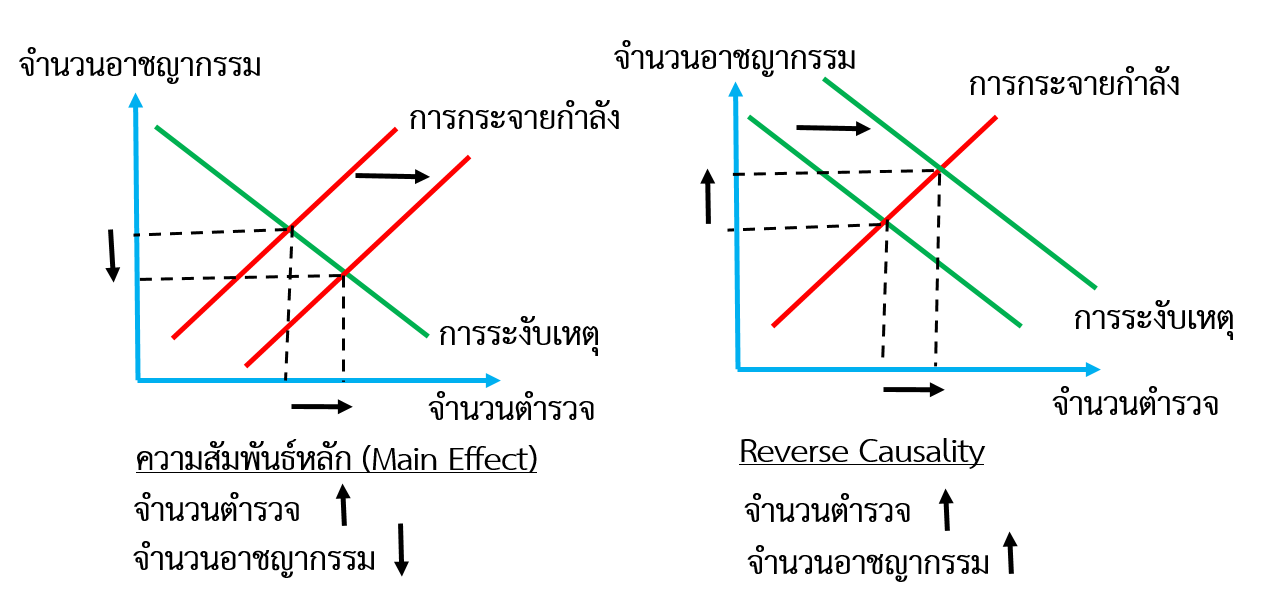
รูปที่ 4 ปัญหา Reverse Causality สำหรับตัวอย่าง “นโยบายการศึกษาภาคบังคับช่วยยกระดับค่าจ้างหรือไม่”

อีกหนึ่งปัญหาที่เกิดขึ้นได้ในการวิเคราะห์ข้อมูล คือ ปัญหาการวัดคลาดเคลื่อน (Measurement Error) ที่เกิดขึ้นกับตัวแปรต้น เช่น สมมติฐานรายได้ถาวร (Permanent Income Hypothesis) โดย Friedman (1957) กล่าวว่า การบริโภคขึ้นอยู่กับรายได้ถาวร เพื่อจะตอบคำถามว่า “การบริโภคเป็นสัดส่วนเท่าใดของรายได้” ปัญหาที่มักเจอ คือ ผู้ตอบแบบสอบถามอาจจะจำไม่ได้ หรือ เจตนาเลี่ยงตอบรายได้ที่เกิดขึ้นจริง

นอกจากนี้ ในหลายอาชีพ รายได้ที่ได้รับในแต่ละช่วงไม่แน่นอน ทำให้รายได้ที่เกิดขึ้นจริงไม่ตรงกับรายได้ถาวร (Hayashi, 2011, Stock and Watson, 2022) ปัจจัยเหล่านี้ทำให้การเก็บข้อมูลรายได้ถาวรคลาดเคลื่อนจากความเป็นจริง Hayashi (2011) ได้แสดงให้เห็นว่า ถ้าข้อมูลรายได้ถาวรมีการวัดคลาดเคลื่อนจากปัจจัยที่กล่าวมา สมการที่ได้จะไม่สอดคล้องกับความสัมพันธ์ที่แท้จริง และ ค่าประมาณของสัดส่วนรายได้ที่ใช้สำหรับการบริโภคจึงต่ำกว่าค่าที่แท้จริง ดังแสดงในรูปที่ 5

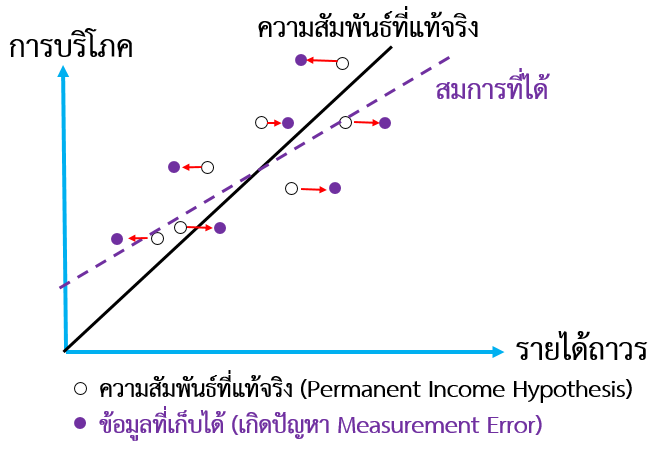
รูปที่ 5 ปัญหาการ วัดคลาดเคลื่อน (Measurement Error) ในการทดสอบสมมติฐาน Permanent Income Hypothesis

จากที่กล่าวมาข้างต้น การที่ผู้ใช้ข้อมูลไม่ได้พิจารณาถึงตัวแปรควบคุมที่สำคัญ (Omitted Variable Bias), ความเป็นไปได้ที่ตัวแปรตามส่งผลต่อตัวแปรต้น (Simultaneity Bias) และ การวัดคลาดเคลื่อน (Measurement Error) ปัญหาเหล่านี้ล้วนทำให้เกิดปัญหาความสัมพันธ์ร่วมกันของข้อมูล (Endogeneity) ซึ่งทำให้ผลลัพธ์ทางสถิติที่ได้สูงกว่าหรือต่ำกว่าความเป็นจริงส่งผลให้การนำข้อมูลไปใช้ผิดพลาด

นอกจากตัวอย่างที่กล่าวมาแล้วข้างต้น เราสามารถนำหลักการเดียวกันนี้มาประยุกต์ใช้ในสถานการณ์อื่นได้ เพื่อเพิ่มความระมัดระวังในการใช้ข้อมูล ไม่ให้การเกิดข้อสรุปที่ผิดพลาดเช่นในกรณีข้างต้น อาทิ ถ้าผู้บริหารต้องการทราบว่า “โฆษณาช่วยเพิ่มยอดขายหรือไม่” จำเป็นต้องตระหนักว่า กลุ่มลูกค้าที่สนใจสินค้าของบริษัทตั้งแต่แรกมีแนวโน้มดูโฆษณาที่มากกว่า ถ้าละเลยปัญหา Simultaneity Bias แล้วจะพบว่าประสิทธิผลของโฆษณาดีกว่าที่ควรจะเป็น (Zantedeschi et al., 2017)

ในกรณีที่นักลงทุนต้องการทราบว่า “ควรลงทุนในกองทุนเชิงรุกหรือกองทุนเชิงรับดีกว่ากัน” จำเป็นต้องตระหนักว่า กองทุนที่มีผลตอบแทนดีกว่าไม่ได้หมายความว่าผู้จัดการกองทุนมีทักษะที่ชำนาญกว่าเสมอไป แต่มักจะเกิดจากปัจจัยความเสี่ยงร่วม (Common Risk Factor) ที่ทำให้อัตราผลตอบแทนที่ต้องการ (Required Rate of Return) แตกต่างกัน ดังนั้น นักลงทุนจำเป็นต้องตระหนักถึงปัจจัยความเสี่ยงเมื่อเปรียบเทียบกองทุนที่มีผลตอบแทนที่แตกต่างกันไป (Carhart, 1997)

วิธีแก้ไขปัญหาปัญหาความสัมพันธ์ร่วมกันของข้อมูล (Endogeneity)

ปัญหาความสัมพันธ์ร่วมกันของข้อมูลทำให้ผลลัพธ์ทางสถิติที่ได้สูงหรือต่ำกว่าความเป็นจริง และ ส่งผลให้การตัดสินใจผิดพลาด วิธีแก้ปัญหาที่หลายท่านมักนึกถึง คือ การทำการทดลอง เช่น การทดลองแบบสุ่มที่มีการควบคุม (Randomized Controlled Trial) และ การทดสอบแบบกลุ่ม (A/B Testing) เช่น Zantedeschi et al. (2017) ใช้ผลลัพธ์จากการทดลองเพื่อศึกษาว่า “โฆษณาช่วยเพิ่มยอดขายหรือไม่”

อย่างไรก็ดี ภายใต้ข้อจำกัดด้านงบประมาณและจริยธรรม การทดลองเพื่อตอบคำถามที่สนใจนั้นมักจะเป็นไปได้ยาก ดังนั้น แทนที่จะอาศัยการทดลองด้วยการปฏิบัติในสถานการณ์จริง นักเศรษฐมิติได้คิดค้นวิธีการที่จะตรวจจับและแก้ไขปัญหาความสัมพันธ์ร่วมกันของข้อมูลด้วยวิธีการทางสถิติ บทความนี้จะขอกล่าวถึง 3 แนวทางสำหรับการแก้ปัญหานี้ด้วยวิธีการทางสถิติเพื่อสร้างความเข้าใจในประเด็นนี้มากยิ่งขึ้น

1. เพิ่มตัวแปรควบคุม (Control Variable)

จากปัญหา Omitted Variable Bias ที่กล่าวไปข้างต้น ถ้าผู้ใช้ข้อมูลไม่ได้ตระหนักถึงตัวแปรควบคุมที่สำคัญ ผลลัพธ์สถิติที่ได้นั้นสูงหรือต่ำกว่าความเป็นจริง จากรูปที่ 1-2 Angrist and Pischke (2009) แสดงให้เห็นว่า ถ้าขาดตัวแปรที่แสดงถึงความสามารถ ผลตอบแทนด้านการศึกษาที่ได้จะสูงกว่าความเป็นจริง เนื่องจากนักเรียนที่มีความสามารถในการเรียนรู้แต่เดิมมีแนวโน้มที่จะศึกษาต่อ และ ได้ค่าจ้างที่สูงขึ้นจากปัจจัยที่มีอยู่เดิม

อย่างไรก็ดี ผู้ใช้ข้อมูลไม่ควรใส่ตัวแปรที่แสดงถึงอาชีพหลังจบการศึกษาในฐานะตัวแปรควบคุม มิเช่นนั้นจะก่อให้เกิดปัญหาความสัมพันธ์ร่วมกันของข้อมูลจากการใส่ตัวแปรเพิ่มโดยไม่ได้พิจารณาอย่างรอบด้าน เนื่องจากอาชีพเป็นผลลัพธ์ที่เกิดขึ้นหลังจากการสำเร็จการศึกษา และ การตัดสินใจเลือกอาชีพสำหรับนักเรียนที่มีระดับการศึกษาแตกต่างกันย่อมไม่เหมือนกัน เช่น นักเรียนที่มีระดับการศึกษาสูงกว่ามีโอกาสเลือกอาชีพที่ใช้ทักษะเฉพาะทางมากกว่า (Angrist and Pischke, 2009)

2. การใช้ตัวแปร Instrumental Variable

จากปัญหา Simultaneity Bias ที่กล่าวไปข้างต้น ในกรณีที่การกระจายตำรวจขึ้นอยู่กับจำนวนอาชญากรรมในพื้นที่นั้น ถ้าผู้ใช้ข้อมูลไม่ได้พิจารณาถึงปัญหานี้ ประสิทธิผลของนโยบายที่คำนวณได้จะต่ำกว่าความเป็นจริง แสดงให้เห็นในรูปที่ 3-4 วิธีแก้ปัญหาที่สามารถทำได้ คือ เลือกข้อมูลบางส่วนที่เข้าข่ายการทดลองตามธรรมชาติ (Natural Experiment) โดยใช้ตัวแปร Instrumental Variable เช่น เพื่อศึกษาผลกระทบของจำนวนตำรวจที่มีต่อจำนวนอาชญากรรมในพื้นที่ Levitt (1997) ศึกษาช่วงเวลาที่มีการเลือกตั้งนายกเทศมนตรีในสหรัฐอเมริกา ค.ศ. 1970-1992 เนื่องจากในช่วงที่จัดการเลือกตั้ง จำนวนตำรวจในพื้นที่เพิ่มขึ้นอย่างมีนัยยะสำคัญ และการศึกษาได้ข้อสรุปว่า การเพิ่มขึ้นของจำนวนตำรวจทำให้จำนวนอาชญากรรมร้ายแรงลดลง นอกจากนี้ Instrumental Variable สามารถใช้แก้ปัญหาการวัดคลาดเคลื่อนในรูปที่ 5 และสามารถใช้ในการทดลองหรือแบบสอบถามได้เช่นเดียวกัน เช่น Ashenfelter and Krueger (1994) และ Gennetian et al. (2005)

3. เพิ่มมิติข้อมูลโดยใช้ Panel Data

ในหลายกรณี ผู้ใช้ข้อมูลมักพบว่าตัวแปรควบคุมบางตัวก่อให้เกิดปัญหาความสัมพันธ์ร่วมกันของข้อมูล แต่การเก็บข้อมูลตัวแปรนั้นทำได้ยาก วิธีแก้ปัญหาที่สามารถทำได้คือการใช้ข้อมูลแผง (Panel Data) หรือข้อมูลช่วงยาว (Longitudinal Data) ซึ่งมีมากกว่าหนึ่งมิติ เช่น มิติเวลา และ มิติบุคคล และใช้วิธีการทางสถิติที่เหมาะสม Fixed-Effect Estimator สำหรับตัวอย่าง “การเพิ่มกำลังตำรวจในพื้นที่ช่วยลดจำนวนอาชญากรรมหรือไม่” Di Tella and Schargrodsky (2004) ใช้เหตุการณ์การโจมตีของผู้ก่อการร้ายซึ่งทำให้กำลังตำรวจเพิ่มมากขึ้นเพื่อสรุปว่าการเพิ่มกำลังตำรวจทำให้จำนวนคดีโจรกรรมยานพาหนะลดลงอย่างมีนัยยะสำคัญ นอกจากนี้ ผู้ใช้ข้อมูลสามารถใช้วิธีการทางสถิติที่ใกล้เคียง Difference-in-Difference เช่น การศึกษาผลกระทบของการขึ้นค่าแรงขั้นต่ำต่อการจ้างงานโดย Card and Krueger (1994) พบว่า การขึ้นค่าแรงขั้นต่ำไม่มีผลต่อการจ้างงานของร้านอาหารจานด่วน

บทสรุป

การตัดสินใจโดยใช้ข้อมูลให้เป็นประโยชน์เป็นทักษะสำคัญในยุคนี้ ในการวิเคราะห์ข้อมูล ผู้อ่านจำเป็นต้องตระหนักถึงปัญหาความสัมพันธ์ร่วมกันของข้อมูล (Endogeneity) ซึ่งเป็นปัญหาที่เกิดขึ้นได้ทั่วไป และ ทำให้ผลลัพธ์ทางสถิติที่ได้นั้นสูงหรือต่ำกว่าความเป็นจริง ซึ่งทำให้เกิดการตัดสินใจที่ผิดพลาดได้ เช่น เพื่อพิจารณาว่า “การเพิ่มกำลังตำรวจในพื้นที่ช่วยลดจำนวนอาชญากรรมหรือไม่” หากผู้ใช้ข้อมูลไม่ได้ตระหนักว่าการกระจายกำลังตำรวจขึ้นอยู่กับจำนวนอาชญากรรมในพื้นที่ จะพบว่านโยบายการเพิ่มกำลังตำรวจได้ผลน้อยกว่าที่ควรจะเป็น (Di Tella and Schargrodsky, 2004) หากผู้บริหารพิจารณาว่า “โฆษณาช่วยเพิ่มยอดขายหรือไม่” และไม่ได้ตระหนักว่าลูกค้ากลุ่มที่รับรู้โฆษณาแตกต่างจากลูกค้ากลุ่มที่ไม่สนใจโฆษณาอย่างชัดเจน จะพบว่าโฆษณาได้ผลเกินกว่าทื่ควรจะเป็น (Zantedeschi et al., 2017) ดังนั้นการตัดสินใจโดยอ้างอิงจากข้อมูลจำเป็นต้องตระหนักถึงปัญหาความสัมพันธ์ร่วมกันของข้อมูล

วิธีการแก้ปัญหาความสัมพันธ์ร่วมกันของข้อมูลนั้นมีหลากหลายรูปแบบ โดยบทความนี้นำเสนอแนวทาง 3 ข้อสำหรับการแก้ปัญหานี้ อย่างไรก็ดี การแก้ไขปัญหาความสัมพันธ์ร่วมกันของข้อมูลยังมีอีกหลายวิธีและค่อนข้างซับซ้อน ขึ้นอยู่กับโจทย์ที่ผู้ใช้ข้อมูลสนใจและระดับความแม่นยำที่จำเป็นต้องใช้ ในทางปฏิบัติ การแก้ปัญหานี้จำเป็นต้องอาศัยความเข้าใจข้อมูลและความรู้เฉพาะสาขา เช่น ความเข้าใจในสภาพสังคมและเศรษฐกิจ (Dell, 2010) และ ทฤษฎีทางเศรษฐศาสตร์ (Sargent, 1976) เมื่อผนวกความรู้เฉพาะสาขากับวิธีการทางเศรษฐมิติที่เหมาะสมแล้ว การตัดสินใจบนพื้นฐานข้อมูลจึงจะแม่นยำ Acknowledgement: ผู้เขียนขอขอบคุณ ดร.ษิฌา ทับทิมพรรณ์ สำหรับข้อเสนอแนะในการเขียนบทความนี้ให้อ่านง่ายยิ่งขึ้น

เอกสารอ้างอิง

Angrist, J. D., & Krueger, A. B. (1991). Does compulsory school attendance affect schooling and earnings?. The Quarterly Journal of Economics, 106(4), 979-1014.

Angrist, J. D., & Pischke, J. S. (2009). Mostly harmless econometrics: An empiricist's companion. Princeton university press.

Ashenfelter, O., & Krueger, A. (1994). Estimates of the economic return to schooling from a new sample of twins. The American economic review, 1157-1173.

Carhart, M. M. (1997). On persistence in mutual fund performance. The Journal of finance, 52(1), 57-82.

Card, D., & Krueger, A. B. (1994). Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania. The American Economic Review, 84(4), 772–793.

Cunningham, S. (2021). Causal inference: The mixtape. Yale university press.

Dell, M. (2010). The persistent effects of Peru's mining mita. Econometrica, 78(6), 1863-1903.

DePrano, M., & Mayer, T. (1965). Tests of the relative importance of autonomous expenditures and money. The American Economic Review, 55(4), 729-752.

Di Tella, R., & Schargrodsky, E. (2004). Do police reduce crime? Estimates using the allocation of police forces after a terrorist attack. American Economic Review, 94(1), 115-133.

Friedman, M. (1957). The permanent income hypothesis. In A theory of the consumption function (pp. 20-37). Princeton University Press.

Gennetian, L. A., Morris, P. A., Bos, J. M., & Bloom, H. S. (2005). Constructing Instrumental Variables from Experimental Data to Explore How Treatments Produce Effects. In H. S. Bloom (Ed.), Learning more from social experiments: Evolving analytic approaches (pp. 75–114). Russell Sage Foundation.

Hayashi, F. (2011). Econometrics. Princeton University Press.

Levitt, S. D., & Snyder Jr, J. M. (1997). The impact of federal spending on House election outcomes. Journal of political Economy, 105(1), 30-53.

Sargent, T. J. (1976). The observational equivalence of natural and unnatural rate theories of macroeconomics. Journal of Political Economy, 84(3), 631-640.

Stock, J. H., & Watson, M. W. (2020). Introduction to econometrics. Pearson.

Tableau. (n.d.). A Guide To Data Driven Decision Making: What It Is, Its Importance, & How To Implement It. https://www.tableau.com/learn/articles/data-driven-decision-making

Tabrizi B., Lam E., Girard K., & Irvin V. (2019). Digital Transformation Is Not About Technology. Harvard Business Review. https://hbr.org/2019/03/digital-transformation-is-not-about-technology

Zantedeschi, D., Feit, E. M., & Bradlow, E. T. (2017). Measuring multichannel advertising response. Management Science, 63(8), 2706-2728.